Difference between revisions of "Template:Frieze group notations"
Jump to navigation
Jump to search
imported>Tomruen |
imported>Lpetrich m (Turned the infinity symbols into Wikipedia markup: ∞ -- Help:Wiki markup) |
||
| Line 11: | Line 11: | ||
![[Schoenflies_notation|Schönflies]]<sup>*</sup> | ![[Schoenflies_notation|Schönflies]]<sup>*</sup> | ||
|- | |- | ||
| − | !p1|| | + | !p1||∞∞||[∞]<sup>+</sup>||C<sub>∞</sub> |
||(hop): Translations only. This group is singly generated, with a generator being a translation by the smallest distance over which the pattern is periodic. Consequently the group is isomorphic to Z, the group of integers. | ||(hop): Translations only. This group is singly generated, with a generator being a translation by the smallest distance over which the pattern is periodic. Consequently the group is isomorphic to Z, the group of integers. | ||
!rowspan=7 align=center|[[File:Frieze2b.png|200px]] | !rowspan=7 align=center|[[File:Frieze2b.png|200px]] | ||
|- | |- | ||
| − | !p11g|| | + | !p11g||∞x||[2<sup>+</sup>,∞<sup>+</sup>]||S<sub>∞</sub> |
||(step): Glide-reflections and translations. This group is generated by a single glide reflection, with translations being obtained by combining two glide reflections. Consequently, this group is also isomorphic to Z. | ||(step): Glide-reflections and translations. This group is generated by a single glide reflection, with translations being obtained by combining two glide reflections. Consequently, this group is also isomorphic to Z. | ||
|- | |- | ||
| − | !p11m|| | + | !p11m||∞*||[2,∞<sup>+</sup>]||C<sub>∞h</sub> |
||(jump): Translations, the reflection in the horizontal axis and glide reflections. This group is isomorphic to the direct product Z × C2, and is generated by a translation and the reflection in the horizontal axis. | ||(jump): Translations, the reflection in the horizontal axis and glide reflections. This group is isomorphic to the direct product Z × C2, and is generated by a translation and the reflection in the horizontal axis. | ||
|- | |- | ||
| − | !p1m1||* | + | !p1m1||*∞∞||[∞]||C<sub>∞v</sub> |
||(sidle): Translations and reflections across certain vertical lines. The elements in this group correspond to isometries (or equivalently, bijective affine transformations) of the set of integers, and so it is isomorphic to a semidirect product of the integers with C2, and isomorphic to the [[infinite dihedral group]]. The group is generated by a translation and a reflection in a vertical axis. It is the same as the non-trivial group in the one-dimensional case | ||(sidle): Translations and reflections across certain vertical lines. The elements in this group correspond to isometries (or equivalently, bijective affine transformations) of the set of integers, and so it is isomorphic to a semidirect product of the integers with C2, and isomorphic to the [[infinite dihedral group]]. The group is generated by a translation and a reflection in a vertical axis. It is the same as the non-trivial group in the one-dimensional case | ||
|- | |- | ||
| − | !p211|| | + | !p211||22∞||[2,∞]<sup>+</sup>||D<sub>∞</sub> |
||(spinning hop): Translations and 180° rotations. Again, the transformations in this group correspond to isometries of the set of integers, and so the group is isomorphic to a semidirect product of Z and C2. The group is generated by a translation and a 180° rotation. | ||(spinning hop): Translations and 180° rotations. Again, the transformations in this group correspond to isometries of the set of integers, and so the group is isomorphic to a semidirect product of Z and C2. The group is generated by a translation and a 180° rotation. | ||
|- | |- | ||
| − | !p2mg||2* | + | !p2mg||2*∞||[2<sup>+</sup>,∞]||D<sub>∞d</sub> |
||(spinning sidle): Reflections across certain vertical lines, glide-reflections, translations and rotations. The translations here arise from the glide reflections, so this group is generated by a glide reflection and a rotation. It is isomorphic to a semi-direct product of Z and C2. | ||(spinning sidle): Reflections across certain vertical lines, glide-reflections, translations and rotations. The translations here arise from the glide reflections, so this group is generated by a glide reflection and a rotation. It is isomorphic to a semi-direct product of Z and C2. | ||
|- | |- | ||
| − | !p2mm||* | + | !p2mm||*22∞||[2,∞]||D<sub>∞h</sub> |
||(spinning jump): Translations, glide reflections, reflections in both axes and 180° rotations. This group is the "largest" frieze group and requires three generators, with one generating set consisting of a translation, the reflection in the horizontal axis and a reflection across a vertical axis. It is isomorphic to C2 × (a semidirect product of Z and C2). | ||(spinning jump): Translations, glide reflections, reflections in both axes and 180° rotations. This group is the "largest" frieze group and requires three generators, with one generating set consisting of a translation, the reflection in the horizontal axis and a reflection across a vertical axis. It is isomorphic to C2 × (a semidirect product of Z and C2). | ||
|- | |- | ||
Revision as of 09:25, 25 June 2011
| Notations | Description | Examples | |||
|---|---|---|---|---|---|
| Intl | Orbifold | Coxeter | Schönflies* | ||
| p1 | ∞∞ | [∞]+ | C∞ | (hop): Translations only. This group is singly generated, with a generator being a translation by the smallest distance over which the pattern is periodic. Consequently the group is isomorphic to Z, the group of integers. | 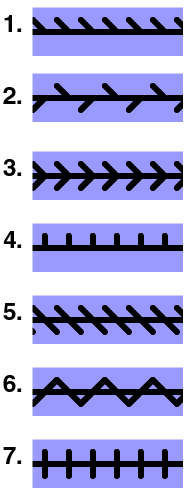
|
| p11g | ∞x | [2+,∞+] | S∞ | (step): Glide-reflections and translations. This group is generated by a single glide reflection, with translations being obtained by combining two glide reflections. Consequently, this group is also isomorphic to Z. | |
| p11m | ∞* | [2,∞+] | C∞h | (jump): Translations, the reflection in the horizontal axis and glide reflections. This group is isomorphic to the direct product Z × C2, and is generated by a translation and the reflection in the horizontal axis. | |
| p1m1 | *∞∞ | [∞] | C∞v | (sidle): Translations and reflections across certain vertical lines. The elements in this group correspond to isometries (or equivalently, bijective affine transformations) of the set of integers, and so it is isomorphic to a semidirect product of the integers with C2, and isomorphic to the infinite dihedral group. The group is generated by a translation and a reflection in a vertical axis. It is the same as the non-trivial group in the one-dimensional case | |
| p211 | 22∞ | [2,∞]+ | D∞ | (spinning hop): Translations and 180° rotations. Again, the transformations in this group correspond to isometries of the set of integers, and so the group is isomorphic to a semidirect product of Z and C2. The group is generated by a translation and a 180° rotation. | |
| p2mg | 2*∞ | [2+,∞] | D∞d | (spinning sidle): Reflections across certain vertical lines, glide-reflections, translations and rotations. The translations here arise from the glide reflections, so this group is generated by a glide reflection and a rotation. It is isomorphic to a semi-direct product of Z and C2. | |
| p2mm | *22∞ | [2,∞] | D∞h | (spinning jump): Translations, glide reflections, reflections in both axes and 180° rotations. This group is the "largest" frieze group and requires three generators, with one generating set consisting of a translation, the reflection in the horizontal axis and a reflection across a vertical axis. It is isomorphic to C2 × (a semidirect product of Z and C2). | |
| |||||