Difference between revisions of "Template:Frieze group notations"
Jump to navigation
Jump to search
imported>Lpetrich (Simplified some of the description, stated abstract groups explicitly, and turned infinity and degree into Wiki markup) |
imported>Tomruen |
||
| Line 6: | Line 6: | ||
!rowspan=2|Examples | !rowspan=2|Examples | ||
|- | |- | ||
| − | ![[ | + | ![[IUC notation|IUC]] |
![[Orbifold notation|Orbifold]] | ![[Orbifold notation|Orbifold]] | ||
![[Coxeter notation|Coxeter]] | ![[Coxeter notation|Coxeter]] | ||
| Line 24: | Line 24: | ||
||(sidle): Translations and reflections across certain vertical lines. The group is the same as the non-trivial group in the one-dimensional case; it is generated by a translation and a reflection in the vertical axis. The elements in this group correspond to isometries (or equivalently, bijective affine transformations) of the set of integers, and so it is isomorphic to a semidirect product of the integers with Z<sub>2</sub>. Abstract group: Dih<sub>∞</sub>, the [[infinite dihedral group]]. | ||(sidle): Translations and reflections across certain vertical lines. The group is the same as the non-trivial group in the one-dimensional case; it is generated by a translation and a reflection in the vertical axis. The elements in this group correspond to isometries (or equivalently, bijective affine transformations) of the set of integers, and so it is isomorphic to a semidirect product of the integers with Z<sub>2</sub>. Abstract group: Dih<sub>∞</sub>, the [[infinite dihedral group]]. | ||
|- | |- | ||
| − | ! | + | !p2||22∞||[2,∞]<sup>+</sup>||D<sub>∞</sub> |
||(spinning hop): Translations and 180° rotations. The group is generated by a translation and a 180° rotation. Abstract group: Dih<sub>∞</sub> | ||(spinning hop): Translations and 180° rotations. The group is generated by a translation and a 180° rotation. Abstract group: Dih<sub>∞</sub> | ||
|- | |- | ||
Revision as of 20:34, 30 June 2011
| Notations | Description | Examples | |||
|---|---|---|---|---|---|
| IUC | Orbifold | Coxeter | Schönflies* | ||
| p1 | ∞∞ | [∞]+ | C∞ | (hop): Translations only. This group is singly generated, with a generator being a translation by the smallest distance over which the pattern is periodic. Abstract group: Z, the group of integers under addition. | 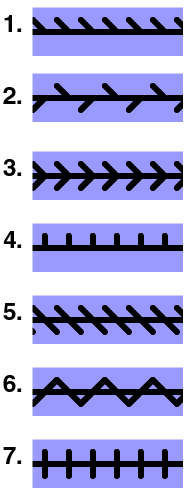
|
| p11g | ∞x | [2+,∞+] | S∞ | (step): Glide-reflections and translations. This group is generated by a glide reflection, with translations being obtained by combining two glide reflections. Abstract group: Z | |
| p11m | ∞* | [2,∞+] | C∞h | (jump): Translations, the reflection in the horizontal axis and glide reflections. This group is generated by a translation and the reflection in the horizontal axis. Abstract group: Z × Z2 | |
| p1m1 | *∞∞ | [∞] | C∞v | (sidle): Translations and reflections across certain vertical lines. The group is the same as the non-trivial group in the one-dimensional case; it is generated by a translation and a reflection in the vertical axis. The elements in this group correspond to isometries (or equivalently, bijective affine transformations) of the set of integers, and so it is isomorphic to a semidirect product of the integers with Z2. Abstract group: Dih∞, the infinite dihedral group. | |
| p2 | 22∞ | [2,∞]+ | D∞ | (spinning hop): Translations and 180° rotations. The group is generated by a translation and a 180° rotation. Abstract group: Dih∞ | |
| p2mg | 2*∞ | [2+,∞] | D∞d | (spinning sidle): Reflections across certain vertical lines, glide reflections, translations and rotations. The translations here arise from the glide reflections, so this group is generated by a glide reflection and either a rotation or a vertical reflection. Abstract group: Abstract group: Dih∞ | |
| p2mm | *22∞ | [2,∞] | D∞h | (spinning jump): Translations, glide reflections, reflections in both axes and 180° rotations. This group is the "largest" frieze group and requires three generators, with one generating set consisting of a translation, the reflection in the horizontal axis and a reflection across a vertical axis. Abstract group: Dih∞ × Z2 | |
| |||||