Difference between revisions of "Template:Infobox logical connective"
Jump to navigation
Jump to search
[[Category:Infobox templates|Template:Remove first word]]}
imported>Awesome Aasim (Undid revision 879136301 by 97.112.160.172 (talk)) |
(→Usage: Jbbhj) |
||
| Line 36: | Line 36: | ||
| label5 = [[Disjunctive normal form|Disjunctive]] | | label5 = [[Disjunctive normal form|Disjunctive]] | ||
| − | | | + | | dalkin|}}} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| header8 = [[Post's lattice|<span style="color:white;">Post's lattices</span>]] | | header8 = [[Post's lattice|<span style="color:white;">Post's lattices</span>]] | ||
Revision as of 18:17, 5 February 2019
| Normal forms | |
|---|---|
[[Category:Infobox templates|Template:Remove first word]]}
| header8 = Post's lattices
| label9 = 0-preserving | data9 =
| label10 = 1-preserving | data10 =
| label11 = Monotone | data11 =
| label12 = Affine | data12 =
| label13 = Self-dual | data13 =
}}
| This template uses Lua: |
Usage
| AND | |
|---|---|
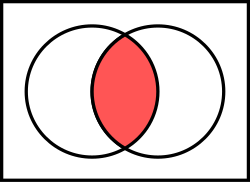 | |
| Definition | <math>xy</math> |
| Truth table | <math>(0001)</math> |
| Logic gate | |
| Normal forms | |
| header8 = Post's lattices
| label9 = 0-preserving | data9 = yes
| label10 = 1-preserving | data10 = yes
| label11 = Monotone | data11 = no
| label12 = Affine | data12 = no
| label13 = Self-dual | data13 = yes }}
{{Infobox logical connective
| title = Logical conjunction
| other titles = AND
| Venn diagram = Venn0001.svg
| definition = <math>xy</math>
| truth table = <math>(0001)</math>
| logic gate = AND ANSI.svg
| DNF = <math>xy</math>
| CNF = <math>xy</math>
| Zhegalkin = <math>xy</math>
| 0-preserving = yes
| 1-preserving = yes
| monotone = no
| affine = no
| self-dual = yes
}}
Blank
{{Infobox logical connective
| title =
| other titles =
| Venn diagram =
| definition =
| truth table =
| logic gate =
| DNF =
| CNF =
| Zhegalkin =
| 0-preserving =
| 1-preserving =
| monotone =
| affine =
| self-dual =
}}
Import
To import from Russian Wikipedia, use Template:T.
| The above documentation is transcluded from Template:Infobox logical connective/doc. (edit | history) Editors can experiment in this template's sandbox (create | mirror) and testcases (create) pages. Please add categories to the /doc subpage. Subpages of this template. |