Template:Frieze group notations
Jump to navigation
Jump to search
↑ Frieze Patterns Mathematician John Conway created names that relate to footsteps for each of the frieze groups.
| IUC | Cox | Schön* Struct. |
Diagram§ Orbifold |
Examples and Conway nickname[1] |
Description |
|---|---|---|---|---|---|
| p1 | [∞]+ |
C∞ Z∞ |
 ∞∞ |
F F F F F F F F hop |
(T) Translations only: This group is singly generated, by a translation by the smallest distance over which the pattern is periodic. |
| p11g | [∞+,2+] |
S∞ Z∞ |
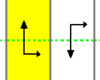 ∞× |
Γ L Γ L Γ L Γ L step |
(TG) Glide-reflections and Translations: This group is singly generated, by a glide reflection, with translations being obtained by combining two glide reflections. |
| p1m1 | [∞] |
C∞v Dih∞ |
 *∞∞ |
Λ Λ Λ Λ Λ Λ Λ Λ sidle |
(TV) Vertical reflection lines and Translations: The group is the same as the non-trivial group in the one-dimensional case; it is generated by a translation and a reflection in the vertical axis. |
| p2 | [∞,2]+ |
D∞ Dih∞ |
 22∞ |
S S S S S S S S spinning hop |
(TR) Translations and 180° Rotations: The group is generated by a translation and a 180° rotation. |
| p2mg | [∞,2+] |
D∞d Dih∞ |
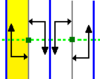 2*∞ |
V Λ V Λ V Λ V Λ spinning sidle |
(TRVG) Vertical reflection lines, Glide reflections, Translations and 180° Rotations: The translations here arise from the glide reflections, so this group is generated by a glide reflection and either a rotation or a vertical reflection. |
| p11m | [∞+,2] |
C∞h Z∞×Dih1 |
 ∞* |
B B B B B B B B jump |
(THG) Translations, Horizontal reflections, Glide reflections: This group is generated by a translation and the reflection in the horizontal axis. The glide reflection here arises as the composition of translation and horizontal reflection |
| p2mm | [∞,2] |
D∞h Dih∞×Dih1 |
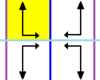 *22∞ |
H H H H H H H H spinning jump |
(TRHVG) Horizontal and Vertical reflection lines, Translations and 180° Rotations: This group requires three generators, with one generating set consisting of a translation, the reflection in the horizontal axis and a reflection across a vertical axis. |
- *Schönflies's point group notation is extended here as infinite cases of the equivalent dihedral points symmetries
- §The diagram shows one fundamental domain in yellow, with reflection lines in blue, glide reflection lines in dashed green, translation normals in red, and 2-fold gyration points as small green squares.